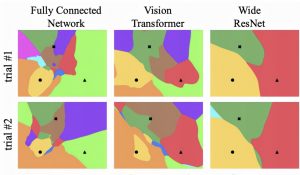
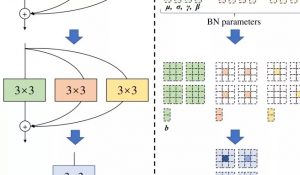
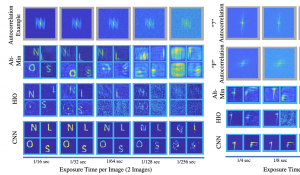
ResNet也能用在3D模型上了，清华「计图」团队新研究已开源
打破2D到3D的壁垒
鱼羊 发自 凹非寺
量子位 报道 | 公众号 QbitAI
用AI处理二维图像，离不开卷积神经网络（CNN）这个地基。
不过，面对三维模型，CNN就没有那么得劲了。
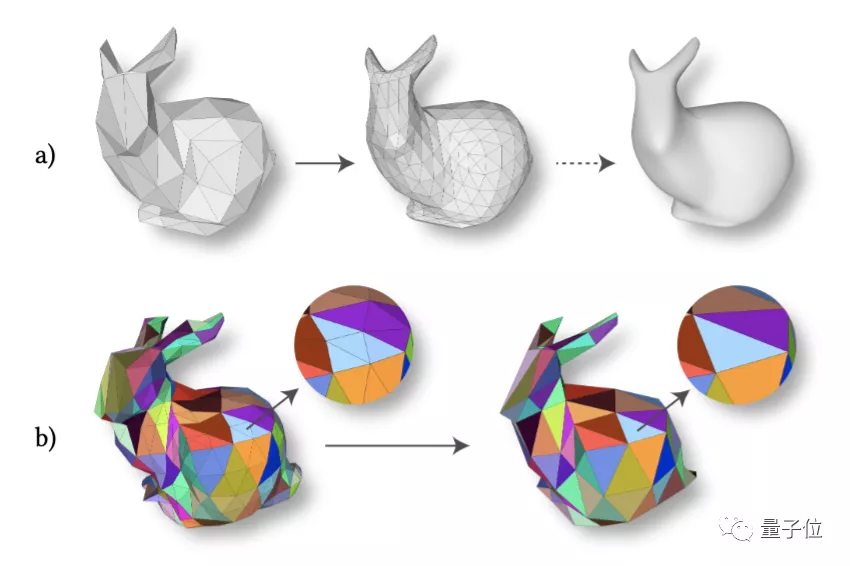
主要原因是，3D模型通常采用网格数据表示，类似于这样：
这些三角形包含了点、边、面三种不同的元素，缺乏规则的结构和层次化表示，这就让一向方方正正的CNN犯了难。
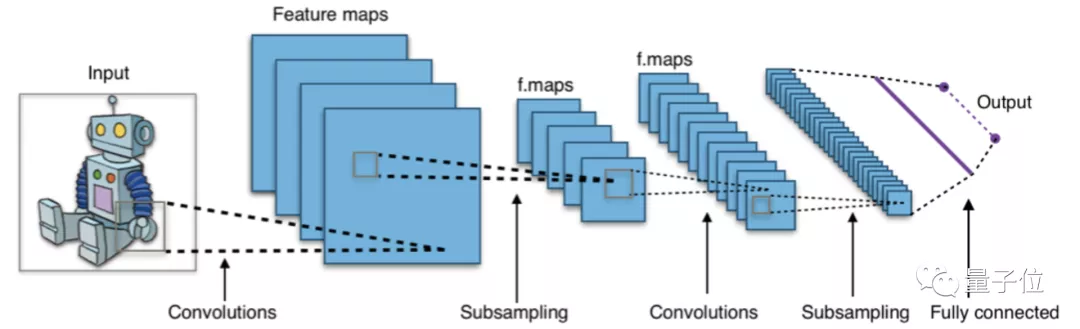
△CNN原理图，图源：维基百科
那么像VGG、ResNet这样成熟好用的CNN骨干网络，就不能用来做三维模型的深度学习了吗？
并不是。
最近，清华大学计图（Jittor）团队，就首次提出了一种针对三角网格面片的卷积神经网络SubdivNet。
基于SubdivNet，就可以将成熟的图像网络架构迁移到三维几何学习中。
并且，相关论文和代码均已开源。
基于细分结构的网格卷积网络
所以，SubdivNet是如何打破2D到3D之间的壁垒的呢？
具体而言，这是一种基于细分结构的网格卷积网络。
对于输入的网格数据，先进行重网格化（remesh），构造细分结构，得到一般网格的多分辨率表示；而后，再上重头戏——面片卷积方法和上下采样方法。
面片卷积方法
以往的网格深度学习方法，通常是将特征存储在点或者边上，这就带来了一个问题：点的度数是不固定的，而边的卷积并不灵活。
于是，计图团队提出了一种在面片上的网格卷积方法，以充分利用每个面片与三个面片相邻的规则性质。
并且，基于这样的规则性质，研究团队进一步依据面片之间的距离，设计了多种不同的卷积模式。
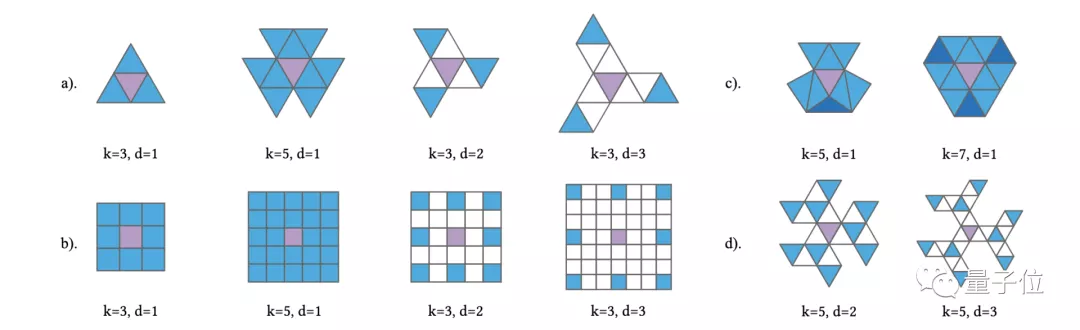
△k为卷积核大小，d为空洞长度
由于三维数据格式中的面片顺序不固定，SubdivNet在计算卷积结果时，通过取邻域均值、差分均值等方式，使得计算结果与面片顺序无关，满足排列不变性。
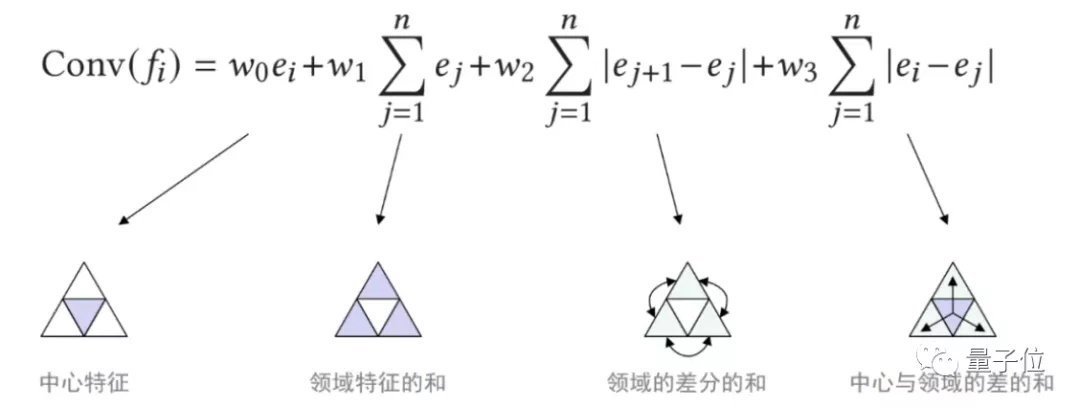
上下采样方法
再来看上下采样的部分。
SubdivNet受到传统的Loop细分曲面建模的启发，构造了一种基于细分结构的上下采样方法。
也就是说，在池化（下采样）过程中，由于网格数据已经经过重网格化，其面片具有细分连接结构，就可以4片变1片，从高分辨率转为低分辨率，实现面片特征的池化操作。
而在上采样的过程中，则反过来，让面片一分为四。
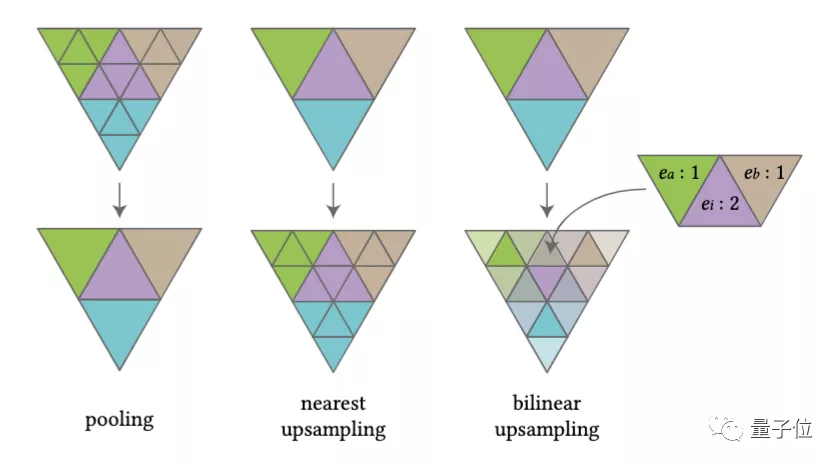
如此一来，上下采样方式就是规则且均匀的，还可以实现双线性插值等需求。
结合面片卷积方法和上下采样方法，像VGG、ResNet、DeepLabV3+这样经典2D卷积网络，就可以轻松迁移到3D模型的深度学习中。
值得一提的是，SubdivNet方法是基于清华大学的深度学习框架计图（Jittor）实现的。其中，计图框架提供了高效的重索引算子，无需额外的C++代码，即可实现邻域索引。
实验结果
至于SubdivNet的效果如何，不妨直接看看实验结果。
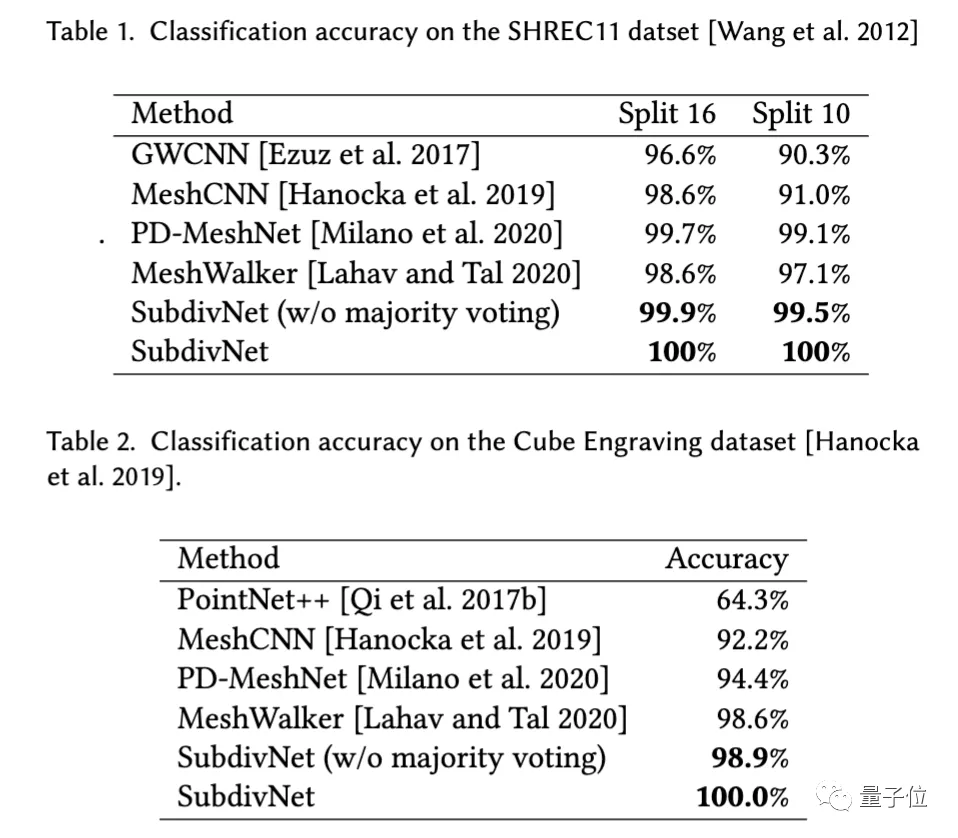
首先，在网格分类数据集上，SubdivNet在SHREC11和Cube Engraving两个数据集中，首次达到了100%的分类正确率。
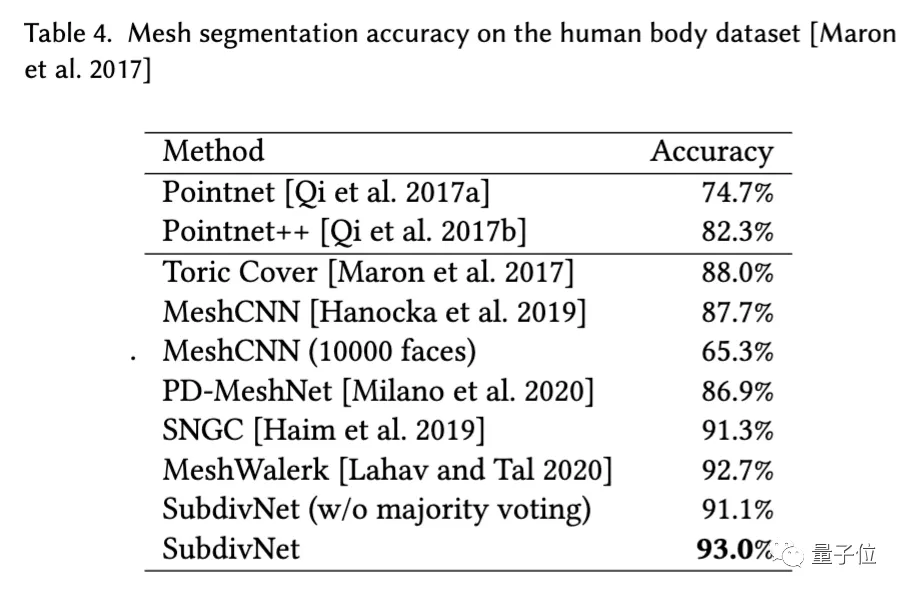
在网格分割方面，量化指标下，SubdivNet的分割准确率均高于用于对比的点云、网格方法。
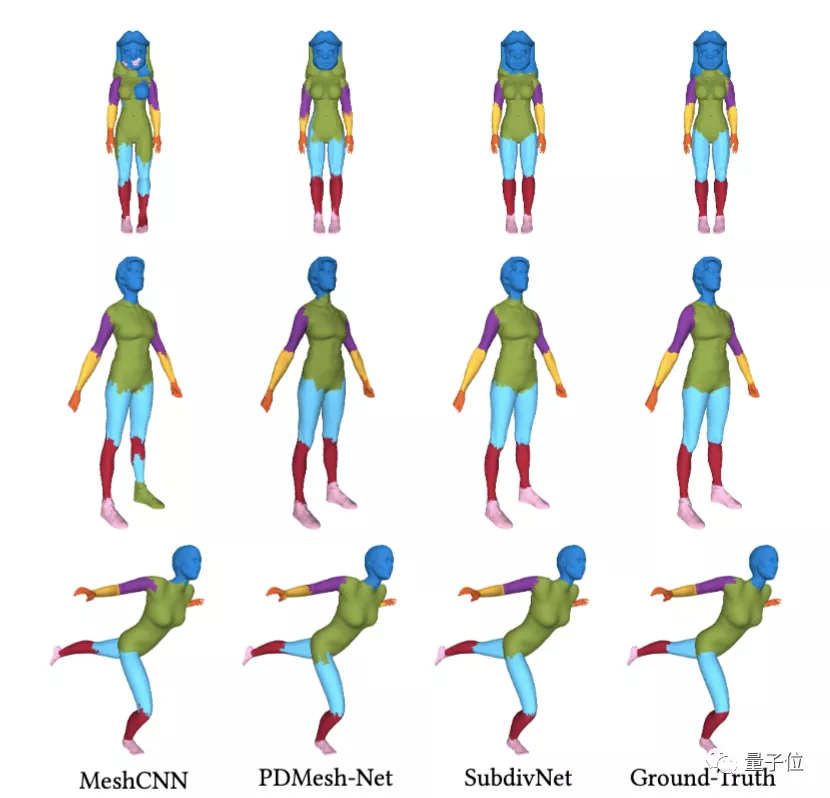
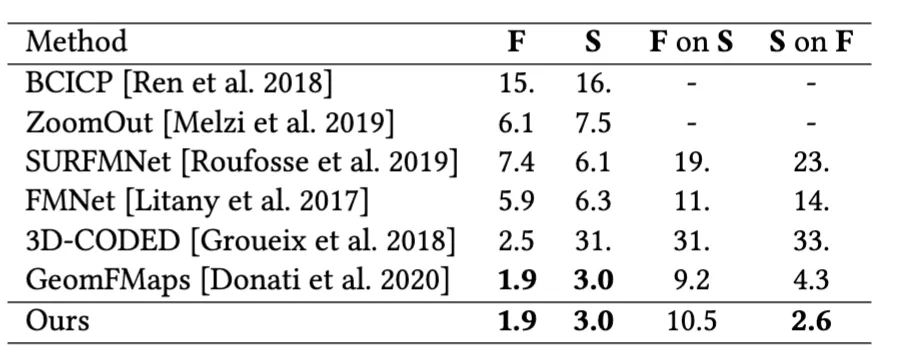
而在形状对应实验中，SubdivNet也达到了SOTA水准。
关于作者
这篇论文来自清华大学计算机系胡事民教授团队。
作者是胡事民及其博士生刘政宁、国孟昊、黄家辉等，还有卡迪夫大学Ralph Martin教授。
同时，他们也是清华“计图”框架团队成员。
计图是首个由中国高校开源的深度学习框架，开发团队均来自清华大学计算机系图形学实验室，负责人是胡事民教授。
该实验室的主要研究方向是计算机图形学、计算机视觉、智能信息处理、智能机器人、系统软件等，在ACM TOG, IEEE TVCG, IEEE PAMI, ACM SIGGRAPH, IEEE CVPR, IEEE ICRA, USENIX ATC等重要国际刊物上发表论文100余篇。
目前，开发计图的主力，是该实验室梁盾、杨国烨、杨国炜、周文洋、刘政宁、李相利、国孟昊和辛杭高等一批博士生。
与TensorFlow、PyTorch不同，计图是一个完全基于动态编译，使用元算子和统一计算图的深度学习框架。
此前，在可微渲染、动态图推理等方面，计图都有超越PyTorch的表现。
论文地址：
https://arxiv.org/abs/2106.02285
项目地址：
https://github.com/lzhengning/SubdivNet
参考链接：
https://mp.weixin.qq.com/s/tJjarzqU7MvS_pHWWO3JYQ
— 完 —
- 0元起步打造你的AI搜索！实测秘塔知识库新功能，竟能指导我升职加薪了2024-11-11
- o1满血版泄露！奥数题图片推理手拿把掐，奥特曼上线剧透o22024-11-03
- 科研版AI搜索来了！知乎直答接入正版论文库，一手实测在此2024-11-01
- 微软清华改进Transformer：用降噪耳机原理升级注意力，一作在线答疑2024-11-03
相关阅读
