陶哲轩破解数十年前几何猜想，用反例证明它在高维空间不成立，同行：推翻的方式极尽羞辱

Pine 萧箫 发自 凹非寺

量子位 | 公众号 QbitAI

又一个重要数学猜想，被陶哲轩和他的博士后破解了！

此前陶哲轩在博客上发了个小预告，就已经有不少人赶来围观：

看起来是个大新闻。

现在，不少人期待的正式版论文，终于在arXiv上新鲜出炉：

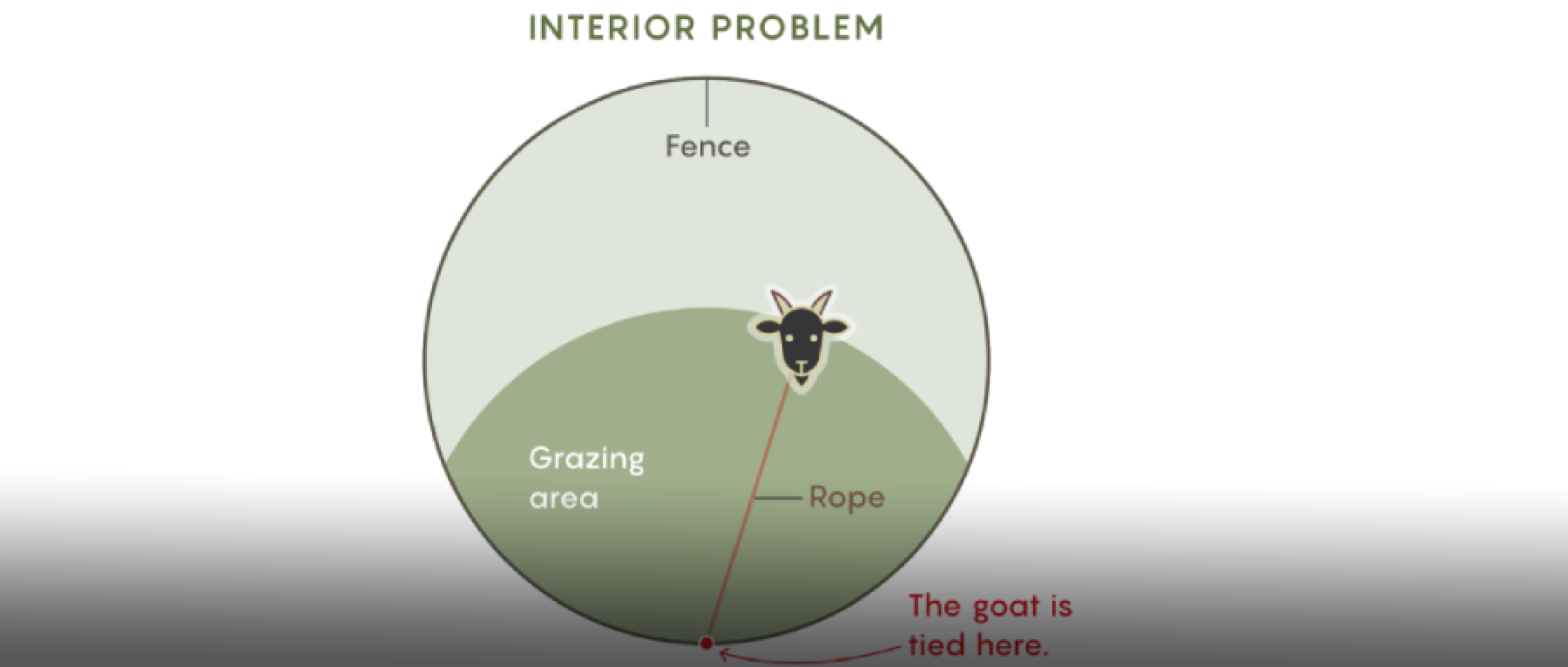
这个猜想，与我们熟悉的“铺瓷砖”问题有关——

用什么样的几何瓷砖，能恰好“天衣无缝”地铺满整个地板平面。

它名叫周期性平铺猜想（periodic tiling conjecture），即在一个平面（plane）中，不存在可以非周期性覆盖整个平面的单个几何图形。

简单来说，就是不存在一个具备“彭罗斯瓷砖”性质的几何图形，它既能通过自身平移或移动（不包括旋转）铺满整个平面，又能让平铺的图案看起来没有“规律性”。

这个猜想曾在二维空间中被证实，因此有数学家认为它同样可以推广到三维、甚至高维空间中去。

但现在，这个猜想在更高维的空间被陶哲轩和他的博士后否定了。

陶哲轩对此表示：

现在大家已经有了新的认知，即高维几何有点让人讨厌（nasty）。

我们从二维和三维空间中获得的直觉，或许会对高维空间的研究产生误导性。

这篇论文出来后，希伯来大学数学名誉教授Gil Kalai发来祝贺：

罗彻斯特大学数学家Alex Iosevich调侃了一下否定猜想的方式：

他们不仅推翻了这个猜想，还是以一种极尽羞辱的方式推翻的。

具体如何？可以一起来看看～

“铺瓷砖”猜想之一，但是高维版

周期性平铺猜想（periodic tiling conjecture），先后在1987年和1996年的两篇论文中被提出。

这一猜想认为，在一个平面（plane）中，不存在可以非周期性覆盖整个平面的单个几何图形。

其中，周期性和非周期性，分别是两种铺满平面的方法。

周期性平铺是一种很有规律的方法，即通过不断重复对某个图案进行“复制-平移-移动”，就能规律性地铺满整个平面：

例如用方块、或是正六边形瓷砖，就能做到非常直观的周期性平铺。

只需要不断复制其中的正六边形或正方形，并进行平移和移动这两种操作，就能轻松铺满整个2D平面：

非周期性的平铺方法，就没那么简单了。

最典型的例子，就是诺贝尔物理学奖得主彭罗斯提出来的“彭罗斯瓷砖”。

他设计了一个瘦四边形（图中红色）和一个胖四边形（图中蓝色），用这两个图形就能铺满整个平面，然而这两个图形究竟是怎么分布的，却没有一个具体的规律可言。

也就是说，用这两种图形铺出来的平面，无法像正方形或正六边形那样，被分割出一块图案“有规律”地进行复制粘贴，而是以一种随机的方式被铺在平面上。

所以，周期性平铺猜想，猜的就是“没有任何一个几何图形，可以靠自身做到非周期性覆盖整个平面”。

一维猜想已经被证实，而就在几年前，数学家Siddhartha Bhattacharya也成功地在二维平面上证明了这个猜想。

于是数学家们大胆了起来，他们猜测——如果周期性平铺猜想放在更高维的平面上，是否同样适用？

这里面，就包括陶哲轩和他的博士后格林菲尔德（Rachel Greenfeld），后者曾在加州大学洛杉矶分校（UCLA）任助理教授，如今去了普林斯顿大学。

至少在发现反例前，他们曾试图证明过高维平面的周期性平铺猜想。

想证明却发现了反例

当格林菲尔德以博士后的身份来到UCLA后，她和陶哲轩便将目光瞄向了周期性平铺猜想。

由于猜想在一维和二维空间被证实，他们决定证明更高维度的猜想，先从三维开始：

如果一个单一的形状可以铺满整个三维空间，那么一定有方法周期性地把它铺满整个空间。

他们甚至为此设计了一个新方法，再次成功证明了二维平面的猜想，但在证明三维空间时却屡屡碰壁。

这时陶哲轩开始思考，是不是高维度下这个猜想是有问题的。

于是，他们俩的研究来了个大转向：开始寻找反例。

解决这个问题时，陶哲轩和格林菲尔德想出了一个大“套路”：先拆解，再各个击破——

将连续无限点阵列拆解成有限点集，将高维问题拆解成低维问题。

为了便于分解，他们尝试重新构建这个问题：将问题设计成一个方程系统，其中未知的变量代表高维空间中所有可能的方法。

而方程系统中的每个方程都表示针对解的不同约束，这样一来，整个高维问题就可以分解成多个不同平面“瓷砖”的问题。

解决“瓷砖”问题的方法也变成了相对容易的计算机编程问题，其中每个命令都是最终平铺所需要满足的不同属性。

而要解决这个问题，就必须保证所有属性的平铺都必须是非周期性的。

以三维空间为例，如果将平面“瓷砖”叠在一起，就能设计出一个适用三维空间的“三明治”结构，每一层瓷砖该如何移动则代表了编程中的属性。放到更高维空间也是如此。

而陶哲轩他们所做的，就是对这些属性进行限制，最终排除掉所有的周期解。

那最终的解又是如何找到的呢？

这又是另外一个难题：网格问题，包含无限数量的行和虽有限但数量依旧庞大的列。

他们有个很巧妙的思路：做“数独”，把网格比作是一个巨大的数独游戏，用特定的数字序列来填充每一行和每一个对角线。

而这些数字序列则需要满足平铺方程的约束条件。

最终，陶哲轩发现了得出的序列是非周期性的，这也意味着平铺方程组的解也是非周期性的。

至此，高维空间的周期性平铺猜想被陶哲轩和他的博士后推翻了。

至于这一反例的维度究竟有多高，陶哲轩给了个大致的范围让大伙“感受感受”：

当然，他们俩的这项工作并不仅仅止于推翻这个猜想，还标志着一种新方法的出现——

它既可以被用来构建一些非周期性平铺猜想，也可以用来推翻其他与瓷砖问题有关的猜想。

就好比说数学家们一般要证明一个猜想是“不可判定”的，通常会证明它等同于另一个已知的“不可判定问题”。

不可判定问题是可计算性理论和计算复杂性理论中定义的一类决定性问题，此类问题无法总是用单一算法得出正确的是/否的答案。

因此，若这个平铺问题被证明是不可判定的，那它便可以作为一个工具来证明在其他情况下一些问题的不可判定性。

论文地址：
https://arxiv.org/abs/2211.15847

参考链接：
[1]https://www.quantamagazine.org/nasty-geometry-breaks-decades-old-tiling-conjecture-20221215/
[2]https://terrytao.wordpress.com/2022/11/29/a-counterexample-to-the-periodic-tiling-conjecture-2/